Инверзија

Инверзија и круг

* Шта је слика круга при инверзији?
Aко круг садржи центар инверзије, онда се он пресликава у праву која не садржи центар инверзије. Ако круг не садржи центар инверзије, онда се он пресликава у круг који не садржи центар инверзије. Прецизније:

* Ако је $ψ_{k}$ инверзија у односу на дати круг $k(O,r)$ тада за сваки круг $l$ у равни $Е^{2}$ важи:
a) ако тачка $O$ припада кругу $l$ , слика тог круга при инверзији $ψ_{k}$ је права $p$
б) ако тачка $O$ не припада кругу $l$ , његова слика је круг $l'$ који је хомотетичан кругу $l$ са центром хомотетије $O$ и коефицијентом $\frac{r^{2}}{p}$ . где је $p$ потенција тачке $O$ у односу на круг $l$ .
Докажимо ово тврђење:
a) Доказ непосредно следи из тога што је инверзија инволуција и што се права која не садржи центар пресликава у круг који садржи центар.

б) Нека је

M

било која тачка на кругу

l

M'

њена слика, тада важи

|ОM|·|ОM'|= r^{2}

. Права

ОM

сече круг у највише још једној тачки

N

. Према дефинцији потенције важи

|ОM|·|ОM'|= p

, где је

p

потенција тачке

O

у односу на круг

l

. Из ове две једнакости следи да је

|ОM'|= \frac{r^{2}}{p} · |ON|

Дакле,

M'

је слика тачке

N

при хомотетији

η

са центром у тачки

O

и коефицијентом

\frac{r^{2}}{p}

.
Како је хомотетична слика круга опет круг, то значи да је скуп

l'

, који је хомотетична слика круга

l

, и сам круг који не садржи центар хомотетије

η

.

* Како конструишемо инверзну слику круга?

Нека је

k

круг инверзије, а

l

круг који пресликавамо.
Ako се кругови

k

l

не секу:
Уочимо праву одређену центрима ових кругова. Нека су

A

B

пресечне тачке те праве и круга

l

. Знамо да конструишемо инверзне слике тачака

A

B

. Tо су тачке

A'

B'

. Тада је тражена слика круга

l

круг

l'

над пречником

A'B'

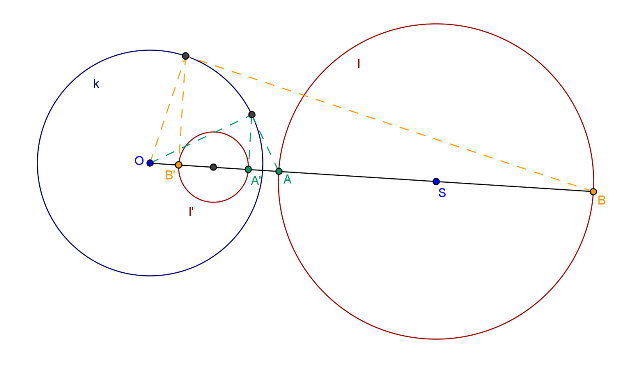
Ako се кругови

k

l

секу:
Нека су пресечне тачке кругова

S_{1}

S_{2}

. Уочимо праву одређену центрима ових кругова, и нека је

A

једна од пресечних тачака те праве и круга

l

. Конструишемо инверзну слику

A'

тачке

A

. Тада је тражени круг

l'

, круг описан око троугла

S_{1} A S_{2}

Ортогонални кругови

Инверзија $ψ_{k}$ у односу на круг $k$ пресликава неки круг $l$ на њега самог ако и само ако су ти кругови $k$ и $l$ једнаки или ортогонални:
$ψ_{k} (l) = l <=>
k$ ⊥ $l$ .
Решење:
Показали смо да је $ψ_{k} (l)$ круг хомотетичан кругу $l = l(S,R)$ са коефицијентом хомотетије $\frac{r^{2}}{p}$ . Дакле,за круг $l ≠ k$ , важи $ψ_{k} (l) = l$ ако и само ако је $\frac{r^{2}}{p} = 1$ тј. $r^{2} = p$ .
Како је $p = {OS}^{2} - R^{2} = p(O,l)$ то је $\frac{r^{2}}{p} = 1$ еквивалентно са тим да је ${OS}^{2} = R^{2} + S^{2}$ што значи да су кругови $k$ и $l$ ортогонални.

Пример
Нека су $l(О,R)$ и $k(S,r)$ описани и уписани круг троугла △ $ABC$ и $l'$ слика круга $l$ при инверзији у односу на круг $k$ . Доказати да је полупречник $r'$ круга $l'$ једнак $\frac{r}{2}$ .
Доказ:
Нека су $E, F, G$ додирне тачке круга $k$ и страница $BC, AB, AC$ . У примеру из поглавља Инверзија и права смо закључили да је:

$ψ_{k} (AB) = k_{1}, k_{1} = k_{1} (SG)$
$ψ_{k} (AC) = k_{2}, k_{2} = k_{2} (FS)$
$ψ_{k} (BC) = k_{2}, k_{3} = k_{3} (SE)$

$A' = ψ_{k} (A) = k_{1}$ ∩ $k_{2}$
$B' = ψ_{k} (B) = k_{1}$ ∩ $k_{3}$
$C' = ψ_{k} (C) = k_{2}$ ∩ $k_{3}$

$ψ_{k} (l) = l'$
па како $l$ ∋ $A, B, C$ закључујемо $l'$ ∋ $A', B', C'$ , тј. $l'$ је круг описан око троугла △ $A'B'C'$ .

Из подударности троуглова △ $AFS$ и △ $AGS$ (која следи из: $|AS| = |AS|, |FS| = |SG| = r,$ ∠ $SFA = 90° =$ ∠ $SGA$ ) закључујемо да је ∠ $FЅА =$ ∠ $АSG$ па је и ∠ $FЅА' =$ ∠ $А'SG$ .
Како важи и $|A'S| = |A'S| и |FS| = r = |SG|$ , следи да је △ $FA'S$ ≅ △ $GA'S$ па је $|FA'| = |A'G|$ .
С друге стране, ∠ $SA'G = 90°$ као угао над пречником $ЅG$ , и угао ∠ $FA'S = 90°$ као угао над пречником $FЅ$ , следи да су $F, A', G$ колинеарне и да је $A'$ средиште $FG$ .
На основу тога закључујемо да је △ $A'B'C'$ сличан △ $ЕFG$ са коефицијентом сличности $\frac{1}{2}$ , одакле следи да је $r' = \frac{r}{2}$ .